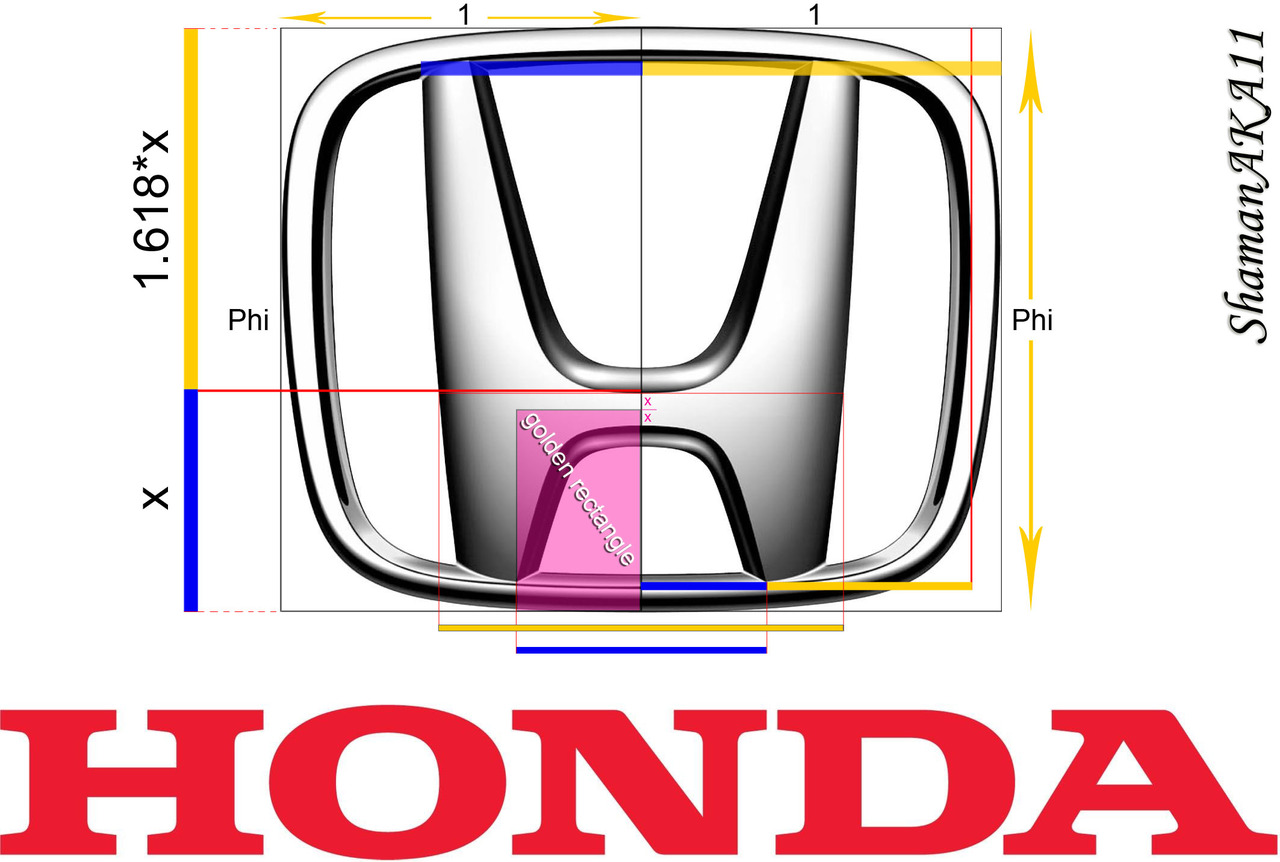
Proporción Áurea.
Primeramente
voy a describir lo que es la proporción áurea.
Es
una razón que existe en la naturaleza, en todo lo material y en el universo
entero, se trata de un extraño número que aparece por ejemplo en el crecimiento
del caracol de mar (nautilus), en los girasoles, en la razón machos y zánganos
en una colmena, entre muchos objetos más.
El número áureo, también
denominado “número de oro, “razón áurea”, “razón dorada”, “media áurea” “divina
proporción” y demás, es el número irracional. Este es designado con letra
griega Φ (fi) = 1,61803... Llamado así porque es la inicial del nombre del
escultor griego Fidias que lo tuvo presente en sus obras, pero el primero en hacer un
estudio formal del número áureo fue Euclides.
Euclides demostró también que este número no puede ser descrito como la
razón de dos números enteros; es decir, es un número irracional.
Platón vivió antes de que Euclides estudiara el número áureo. Sin embargo,
a veces se le atribuye el desarrollo de teoremas relacionados con el número
áureo. Es un número tan peculiar que hasta tiene un nombre propio y un símbolo
para representarlo pero también es cierto que no es el único número peculiar,
hay algunos más con su propio nombre y símbolo como p, al que conocemos desde
la enseñanza elemental.
Al igual que p, la razón áurea es
un número que expresa una razón, es decir, el cociente de otros dos números. La
magia de p es que esta razón es la misma sin importar qué tan grande sea el
círculo.
Dicho número posee muchas
propiedades interesantes y fue descubierto en la antigüedad, no como “unidad”
sino como relación o proporción entre partes de cuerpos, que como lo
mencionamos antes lo encontramos en la naturaleza, en la morfología de diversos
elementos, el grosor de las ramas, proporciones humanas, etc. Está relacionada
directamente con una proporción que se encuentra en la naturaleza, pero también
en las figuras geométricas.
Es un descubrimiento del
ser humano y sus aplicaciones en el arte una forma de crear, o intentar, crear
belleza.
Se dice que el rostro
humano es reflejado en proporciones con el número de “oro” pero muchas personas
no están de acuerdo con este número. La belleza tiene algo que ver con este
descubrimiento matemático. Todas las personas tenemos diferentes tipos de rostros,
diferentes proporciones pero se clasifican con más belleza los que tienen la
proporción aurea.
Por otra parte, se muestra
que en un punto de luz los insectos trazan una espiral logarítmica, una espiral
áurea que siempre es la misma porque es la única en la que siempre conservan el
mismo ángulo de giro, la misma espiral que dibujan las aves de presa cuando se
lanzan a cazar, la única con la que pueden mantener la cabeza recta manteniendo
siempre el control visual sobre las presas y maximizando la velocidad.
El número phi se halla en
el mismo cuerpo humano del cual, si tuviésemos que extraer una medida ideal, lo
haríamos calculando la media entre todos los cuerpos medidos. Ciertos estudios estadísticos
demuestran que la media en la medida de la altura total de un cuerpo humano y
la distancia desde el suelo al ombligo revelan esta proporción: si asignamos el
valor 1 a la distancia del pie al ombligo la altura total del cuerpo sería de
1,61.
Matemáticamente hablando…
Matemáticamente hablando…
El número de oro tiene
infinitos números decimales, pero al usarlo generalmente se utilizan más pocos
de ellos. Con él se resuelven ecuaciones de segundo grado.
Leonardo Pisano, conocido
como Fibonacci, fue un famoso matemático italiano que difundió por Europa el
sistema de numeración árabe con base decimal y con un valor nulo (el cero).
Pero el gran descubrimiento de Fibonacci fue la Sucesión de Fibonacci que,
posteriormente, dio lugar a la proporción áurea.
¿Qué es la Sucesión de
Fibonacci? Se trata de una serie númerica : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Es una serie infinita en la que la suma de dos números consecutivos siempre da
como resultado el siguiente número (1+1=2; 13+21=34). La relación que existe
entre cada pareja de números consecutivos es decir, si dividimos cada número
entre su anterior, se aproxima al número áureo (1,618034) que se identifica con
la letra Phi del abecedario griego.
Desde la admiración de los
pitagóricos por el pentágono estrellado hasta la construcción de cúpulas
geodésicas derivadas del icosaedro, siempre ha tenido ese carácter oculto,
contemplativo, abstracto, tan atractivo para los amantes de la geometría y las
matemáticas. Sin embargo, es un sistema muy compacto; allí donde aparece está
en todas partes. Para construir el pentágono regular, bien a partir del lado
base, bien circunscrito en una circunferencia, siempre tenemos que recurrir a
la proporción áurea.
El Pentagrama pitagórico
Los pitagóricos adoptaron como símbolo el Pentágono regular estrellado. Su propiedad
geométrica es que todos los segmentos están en progresión áurea.
El triángulo del pentalfa,
también llamado Triángulo Sublime y Triángulo áureo mayor, tiene sus lados en
proporción áurea, y sus ángulos en razón simple 1:2:2. Aparece en diversas
formas en el pentágono y el decágono:
En el universo, la
naturaleza, en todas las cosas incluyendo en nosotros mismos existe algo
llamado el "número áureo", también se conoce como la divina proporción.
Esta presente en todas las cosas creadas.
En el rostro, si divides
la distancia que hay entre el inicio de la nariz y la barbilla por la altura de
la frente obtienes el numero Fi.
La distancia que hay entre
la comisura de los labios y la barbilla por la distancia que hay del final de
la nariz esa comisura obtienes el número
de oro.
Si divides la altura de la
cara por la distancia que hay entre los extremos de las cejas también obtenemos
Fi.
Aunque su definición
resulte abstracta y algo difícil de entender, la aplicación de la proporción
áurea es importante en la fotografía, la pintura, la escultura y otras artes
que suelen vincular el ideal de belleza a las simetrías y las proporciones.
El rectángulo áureo
Una manera de explicar la
proporción áurea es en un rectángulo. A continuación se muestra.
En el rectángulo se dibuja
un cuadrado y se marca el punto medio de uno de sus lados. Lo unes con uno de
los vértices del lado opuesto y llevas esa distancia sobre el lado inicial, de
esta manera se obtiene el lado mayor del rectángulo.
Si el lado del cuadrado
vale 2, el lado mayor del rectángulo vale 1+√5 por lo que la
proporción entre los dos lados nos da como resultado el número de oro.
Obtenemos así un
rectángulo cuyos lados están en proporción áurea. A partir de este rectángulo
podemos construir otro tipo de objetos, como sería edificios, esculturas,
escaleras, muebles etc.
La proporción aúrea es
tenida en cuenta en el diseño de numerosos objetos cotidianos. Las tarjetas de identificación
no tienen las dimensiones que tiene por casualidad, se diseñó según un
rectángulo aúreo, y como los distintos objetos de nuestro alrededor se logra comprobar la existencia del número de oro.
Tarjeta de crédito, tarjetas
de presentación… Estos tipos de tarjeta tienen las mismas dimensiones y son un
rectángulo aúreo. ¿Creías que se trataba de un rectángulo cualquiera? Pues ya
sabes que no. Para comprobar que es aúreo, sólo hay que dividir el lado más
grande entre el lado más pequeño y comprobar que el resultado es
aproximadamente s1.62
La razón áurea se utilizó
mucho en la época del renacimiento en especialmente en las esculturas, en las
obras plásticas y en la arquitectura. Un personaje claro de esta época es Da
Vinci, quien en esa época realizo con varias ilustraciones llamado “De divina
proporcione” estas ilustraciones están hechos en base con los cinco sólidos.
Los artistas de esta época se basaron bastante en el número de oro para la
escritura, arte, y arquitectura en varias ocasiones. Una obra conocida por Da
Vinci en esa época es la última cena conocida entre los católicos como la
representación de Jesús un día antes de que fuera crucificado, cenando con sus
discípulos, so observamos esta pintura, se aprecia con bastante belleza y
naturaleza, ya que fue ella con el número de oro, y esto lo descubrió Johanes
Kepler ya que se dedicó a estudiarla y analizarla y con base descubrió que fue
hecha con el número de oro (también así conocido). La proporción áureo número
de oro se estudió desde la antigüedad, ya que aparece regularmente en la
geometría, en los patrones de crecimiento de órganos y organismo bilógicos
industriales.
Después de haber descrito
el rectángulo áureo, nos queda claro que es una proporción utilizada en todo lo
que nos rodea.
Como un ejemplo de esto es
una cajetilla de cigarros, con las medidas exactas para ser atractivas, sin
embargo sabemos que nos es dañino para la salud.
Con el paso de los años no
todos los expertos han estado de acuerdo con que el número de oro coincida o
que se base para que algo este realmente bello. Cabe mencionar que muchas de
estas afirmaciones por parte de distintos grupos carecen de información concreta
que apoye sus términos sin embargo existen personas de alto criterio del cual
se puede confiar en sus teorías creyente o no de la razón áurea y su aplicación
en el arte, la naturaleza y arquitectura. Tal es el caso del Dr. George
Markowsky que en ocho conceptos erróneos de la proporción áurea propuestos por
el mismo intenta aclarar algunas dudas. Según su análisis dice que la
proporción aurea es simple pero siempre sus resultados son erróneas o
incompletas, ya que la medición de los objetos solo pueden ser aproximaciones.
Nos cuenta que no solo en
construcciones u objetos se usa esta razón de oro, si no que últimamente estaba
siendo llevada para la elaboración de diseños faciales. Otra cosa, que dice es
que el rectángulo que use esta proporción es más atractivo.
El Dr. comienza hablando de que la razón no puede
expresarse en el medio físico tal y como se pudiera expresar teóricamente, por
lo que son solo aproximaciones. El propone una guía, donde dice: “Voy a
considerar una demanda de la proporción áurea sea al menos razonable si la
relación calculada está dentro de aproximadamente el 2% de Φ ". Esto se
refiere a que pude haber una ligera variación en la proporción de los objetos.
Luego propone algo más:
“Puesto que el rango de aceptación incluye un número infinito de números cerca
de Phi es necesario para justificar que la afirmación de que Phi es el número
preferido. Alguna otra relación casualmente cerca de Phi podría ser el
importante”. Esto suena más razonable según el artículo, pero menciona que por
parte de esto el trabajo empieza a perder validez. Porque se comienza a tomar a
Φ, como “un número infinito de otros números”, olvidando que solo es un cierto
número establecido.
Sin embargo existe quienes consideran a la razón aurea como falsa.
Y en muchos sitios de internet se muestran asi:
“Los sinsentidos sobre Fibonacci”
Una búsqueda en internet, o en su biblioteca local lo convencerá de que la
serie de Fibonacci ha atraído a más de un lunático que busca el misticismo en
los números. Se puede encontrar con afirmaciones fantásticas como estas:
Los "rectángulos de oro" son los "más bello"
rectángulos, y los utilizaron deliberadamente los artistas en sus pinturas. (Se
podría pensar que siempre utilizaban marcos rectángulares áureos, pero no lo
hacían).
Los modelos basados en los números de Fibonacci, el número áureo y el
rectángulo de oro son los más agradables a la percepción humana.
Mozart utilizó Φ en la composición de su música. (A él le gustaban los
juegos de números, pero no hay buena evidencia de que alguna vez utilizara
deliberadamente a Φ en una composición).
La secuencia de Fibonacci se ve en la naturaleza, en la disposición de las
hojas sobre el tallo de las plantas, en el patrón de las semillas de girasol,
en las espirales de los caracoles, en el número de pétalos de las flores, en
los períodos de los planetas del sistema solar, e incluso en los ciclos del
mercado de valores. ¡Tan omnipresente es la secuencia en la naturaleza (de
acuerdo con esta gente) que uno empieza a sospechar que la serie tiene la
notable capacidad de "ajustarse" a casi cualquier cosa!
Los procesos de la naturaleza son "gobernados" por el número
áureo. Inclusive, algunas fuentes dicen que los procesos naturales se
"explican" por esta relación.
Por supuesto, gran parte de esto es completamente absurdo. Las matemáticas
no "explican" lo que sea en la naturaleza, sino que usa modelos
matemáticos muy potentes para describir los patrones y las leyes de la
naturaleza. Creo que es seguro decir que la secuencia de Fibonacci, la
proporción dorada, y el rectángulo de oro, jamás han conducido de manera
directa al descubrimiento de una ley fundamental de la naturaleza. Cuando vemos
un patrón numérico o geométrico ordenado en la naturaleza, nos damos cuenta que
hay que cavar más profundo para encontrar la razón subyacente de por qué estos
patrones emergen."
"¿Secuencias de Fibonacci en la naturaleza? Filotaxis. El diccionario define filotaxis
como la historia o el curso de la evolución de algo. En biología, generalmente
se refiere a cómo un ser vivo se desarrolla y cambia con el tiempo. Esta es una
parte de la naturaleza, donde la secuencia de Fibonacci y las secuencias
relacionadas parecen mostrarse muy a menudo y es legítimo preguntarse por qué.
Los casos interesantes son las inflorescencias de las plantas, las semillas en
el girasol y los patrones en las brácteas de las piñas.
Hemos señalado anteriormente que no todas las espirales en matemáticas o en
la naturaleza son espirales de oro. Del mismo modo, las espirales pueden ser
producidos por procesos no biológicos, si los elementos individuales que componen
la espiral se establecen de acuerdo a algunas reglas simples. El problema para
los biólogos es encontrar esas reglas. La mera afirmación de que "la
naturaleza parece preferir los números de Fibonacci" (la mayor parte del
tiempo, en algunos casos particulares) no es una explicación.
Si bien es cierto, el
universo esta creado muy perfectamente y en el, hay muchísimas cosas creadas
por el número de oro que nos parecen más bonitas y llaman más nuestra atención.
Es algo muy increíble ya
que fue creado por el humano, y nos indica que hay mucha inteligencia en
nosotros solo es cuestión de investigar y adentrarnos en el conocimiento.
Este es un tema muy
extenso y puedes creerlo o no, porque hay diferentes argumentos convincentes y
otros que no tanto, sin embargo es decisión de cada persona.